

%20A%20Description%20of%20the%20Weydenhammer%20Portrait%20Fragment.jpg)
JOBIN versus LEHMAN
Dans Early Music de février 2005 est paru une découverte majeure : l'explication du graphisme accolé au titre du Clavecin bien-tempéré (CBT) qui donne, de la main même de J.S. Bach, la clef de l'accord "bien-tempéré".
Cette découverte expliquée
par Bradley Lehman (voir également sur son site http://www.larips.com/
) s'est trouvée contestée par Emile Jobin et ses collègues
du C.N.S.M.D de Paris.( voir "http://www.clavecin-en-france.org/BACH-et-le-Clavier-bien-Tempere").
Voici, après quelques rappels de tempéraments usuels, les caractéristiques
de la découverte sensationnelle de Lehman, ainsi que l'interprétation
de Jobin et mes doutes quand à la validité de sa lecture.
N'hésitez à me faire part de vos impressions à allain-dupre@club-internet.fr
Tableau donnant les écarts par rapport au tempérament égal (chiffres en cents)
|
Tempérament |
DO |
DO # |
Ré |
MI b |
MI |
FA |
FA # |
SOL |
SOL # |
LA |
SI b |
SI |
|
Werkmeister 3 |
0 |
-10 |
-8 |
-6 |
-10 |
-2 |
-12 |
-4 |
-8 |
-12 |
-4 |
-8 |
|
Kirnberger 3 |
0 |
-10 |
-6 |
-6 |
-14 |
-2 |
-10 |
-3 |
-8 |
-10 |
-4 |
-12 |
|
Mésotonique au 1/4 c |
0 |
-24 |
-7 |
+10 |
-14 |
+3 |
-21 |
-3 |
-27 |
-10 |
+7
|
-17 |
|
Rameau (1726) d'après Gallimard |
0 |
-13.5 |
-7 |
-2 |
-14 |
+3.5 |
-15.5 |
-3,5 |
-11.5 |
-10.5 |
+7 |
-17.5 |
|
Interprétation Jobin de la spirale du CBT |
0 |
-13.5 |
-7 |
-8 |
-14 |
-2 |
-15.5 |
-3.5 |
-11.5 |
-10.5 |
-5 |
-17.5 |
|
Valloti &Young |
0 |
-6 |
-4 |
-2 |
-8 |
+2 |
-8 |
-2 |
-4 |
-6 |
0 |
-10 |
|
CBT Lehman au 1/6 de c. pythagoricien. |
0 |
-2 |
-4 |
-2 |
-8 |
+2 |
-4 |
-2 |
-2 |
-6 |
-2 |
-6 |
|
CBT Lehman au 1/6 de c. syntonique. |
0 |
-0.4 |
-3.2 |
-0.4 |
-6.4 |
+1.6 |
-2.4 |
-1.6 |
-0.4 |
-4.8 |
-0.4 |
-4.4 |
1 comma syntonique = 22 cents (4qtes= 4x2cts - tierce pure=-14cts) 4x2-(-14)=22 cents
1 comma pythagoricien = 24 cents (12 quintes = 12x2)
1 schisma = 2 cents = 1/12 de comma pythagoricien = différence entre quinte pure et tempérée
Quelques tempéraments usuels :
Werkmeister III : 8 quintes pures sauf do-sol, sol-ré, ré-la, si-fa# réduites de 1/4 de comma pyth. tierces bonnes sauf fa#sib, do#fa et sol#do
Vallotti (Padoue 1779) et Young (Londres 1800): 6 quintes pures sur fa#, do# sol#, mib, sib, Fa et 6 quintes do-sol-re-la-mi-si-fa# réduites de 1/6 de comma (Vallotti décale en partant du fa).
Kirnberger III : 1 tierce pure do-mi (les 4 quintes la composant réduites de 1/4 de comma syntonique) les autres quintes pures sauf fa#-do# tempérée
Rameau : 4 tierces pures, sib-ré, fa-la, do-mi et sol-si. 7 quintes petites (-1/4 de comma synt ), celles sur si, fa#, do# sont pures et celles sur sol# et mib trop grandes de 1/3 de comma
Bach (Clavier Bien Tempéré) d'après Bradley Lehman (découverte en 2004, Early Music fév 2005) : 5 quintes petites (-1/6 de comma pythagoricien), sur fa, do, sol, ré, la, 3 quintes pures sur mi, si, fa#, 3 quintes sur do# sol# et mib trop petites de 1/12 de comma et sib-fa trop grande de 1/12 de comma. Si l'on prend le comma syntonique comme base de correction, cette quinte est pure..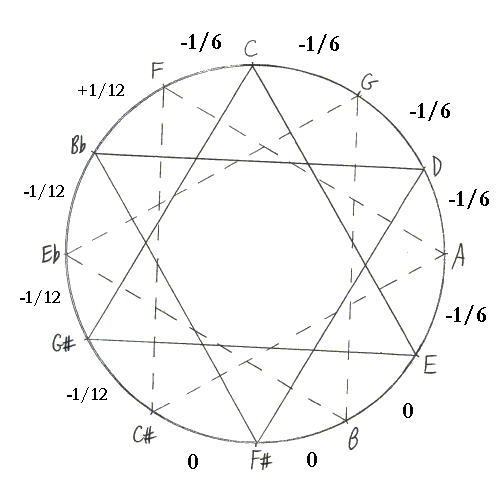
Cycle des quintes de Bradley Lehman en prenant le comma pythagoricien comme base .
Si l'on prend le comma syntonique comme
base de correction, il n'y a pas besoin de rajouter de schisma entre sib et
fa , cette quinte est pure (0). Ce semble être le choix logique si l'on
considére que le tempérament de Bach est un Tartini-Valotti amélioré.
Mais Bradley Lehman semble préférer la version pythagoricienne,
et Bach lui-même semble proposer l'alternative (voir plus loin la discussion
sur la signification de ![]() et
et![]() .)
.)
LaripS (spiral à l'envers) de Bradley Lehman, retournée dans le sens où Bach l'a tracée, de gauche à droite :
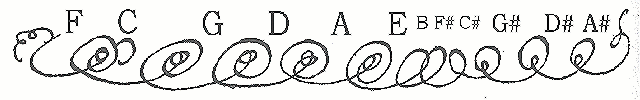
Bach Jobin (interprétation libellée "CNSMD de Paris" en mai 2005) : 2 tierces pures do-mi et sol-si, 5 quintes petites en partant du do (-1/4 de comma syntonique), celles sur si, fa#, do# sont pures et celles sur sol# mib et si b trop grandes d'environ 1/20 de comma. La dernière quinte fa do est pure.
Cela équivaut à un Rameau amélioré, où le ré# et le la# sont moins hauts que chez le français. (voir comparaison en gras sur le tableau)
Beaucoup de tonalités inabordables. Ce n'est pas bien tempéré pour les tonalités éloignées de do majeur.
Il y a plusieurs fautes de lecture de la spirale par Jobin, dues sans doute, comme le fait remarquer Lehman, à la mauvaise qualité de ses reproductions de la spirale :
-le C est après la 1ère boucle, aussi Lehman a interprété cette boucle comme étant la correction de la quinte fa-do. Si l'on considère comme Jobin que c'est la correction de la quinte sur do alors on décale tout d'une quinte . Pourquoi pas? mais fa-do devient pur ou même plus grand que pur. Ce n'est pas très intéressant. Ce sont les quintes sur mi, si, fa# qui sont pures chez Lehman. Avec Jobin ce sont celles celles sur si, fa#, do#. Du fait de la pureté des tierces do-mi et sol-si, et donc de la petitesse des 5 quintes de do à si, ces deux dernières notes fa# et do# sont beaucoup trop basses pour avoir un solb ou un réb correct.
-L'inversion de calligraphie des boucles 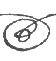 et
et ![]() n'exprime pas leur différence
de sens (5 plus petites, 3 plus grandes, comme dit Jobin) mais leur rang d'importance
: la réduction des 5 premières quintes est primordiale, comme
dans tous les systèmes au 1/6ème de comma, donc la
double accolade est dessinée en premier, car c'est la base de la réalisation
de la partition.
n'exprime pas leur différence
de sens (5 plus petites, 3 plus grandes, comme dit Jobin) mais leur rang d'importance
: la réduction des 5 premières quintes est primordiale, comme
dans tous les systèmes au 1/6ème de comma, donc la
double accolade est dessinée en premier, car c'est la base de la réalisation
de la partition.
En revanche, l'égalisation des 3 dernières quintes sur do#, sol#
et ré# se fait à la fin de la partition, donc Bach a dessiné
la petite boucle ![]() après la grande.
En fait ces huit quintes sont rétrécies. C'est une faute de lecture
de Jobin de les voir corrigées dans des directions opposées. Si
Bach avait voulu schématiser des quintes plus grandes que pures, il aurait
logiquement placé cette petite boucle à l'extérieur du
cercle de la pureté.
après la grande.
En fait ces huit quintes sont rétrécies. C'est une faute de lecture
de Jobin de les voir corrigées dans des directions opposées. Si
Bach avait voulu schématiser des quintes plus grandes que pures, il aurait
logiquement placé cette petite boucle à l'extérieur du
cercle de la pureté.
Je pense que la dernière petite boucle à gauche ![]() exprime
la pureté "hypothétique" (ce pourquoi elle part en l'air) de la
dernière quinte sib-fa. Cette pureté est réalisée
dans la version syntonique du tempérament Lehman (voir ci-dessus). Comme
l'a bien démontré Lehmann, le dessin se fait de gauche à
droite, la page de titre étant retournée, et il est donc bien
improbable que Bach ait essayé d'écrire un f à l'envers
pour placer le Fa. C'est très difficile à dessiner à la
plume en montant.
exprime
la pureté "hypothétique" (ce pourquoi elle part en l'air) de la
dernière quinte sib-fa. Cette pureté est réalisée
dans la version syntonique du tempérament Lehman (voir ci-dessus). Comme
l'a bien démontré Lehmann, le dessin se fait de gauche à
droite, la page de titre étant retournée, et il est donc bien
improbable que Bach ait essayé d'écrire un f à l'envers
pour placer le Fa. C'est très difficile à dessiner à la
plume en montant.
Le petit dessin de droite,![]() lui de
calligraphie vraiment inversée car il faut retourner la page et reprendre
la plume pour le dessiner, exprime l'excès possible d'environ 1/12ème
de comma sur cette dernière quinte, si l'on a bien réduit les
cinq quintes de l'hexachorde (de fa à mi) de1/6 de comma pythagoricien.
1/12ème de comma, c'est le schisma, différence entre la quinte
pure et la quinte tempérée ou aussi différence entre le
comma syntonique et le comma pythagoricien. Ce graphisme peut aussi signifier
: "et ainsi de suite pour les octaves". Si Jobin trouve l'interprétation
de Lehmann sophistiquée, que dire de cette lecture cow
comme signifiant un
"C pur 3", donc une tierce pure sur do? C'est complétement tiré
par les cheveux, et c'est malheureusement la base de toute la démonstration
de Jobin.
lui de
calligraphie vraiment inversée car il faut retourner la page et reprendre
la plume pour le dessiner, exprime l'excès possible d'environ 1/12ème
de comma sur cette dernière quinte, si l'on a bien réduit les
cinq quintes de l'hexachorde (de fa à mi) de1/6 de comma pythagoricien.
1/12ème de comma, c'est le schisma, différence entre la quinte
pure et la quinte tempérée ou aussi différence entre le
comma syntonique et le comma pythagoricien. Ce graphisme peut aussi signifier
: "et ainsi de suite pour les octaves". Si Jobin trouve l'interprétation
de Lehmann sophistiquée, que dire de cette lecture cow
comme signifiant un
"C pur 3", donc une tierce pure sur do? C'est complétement tiré
par les cheveux, et c'est malheureusement la base de toute la démonstration
de Jobin.
Ce sont des détails. La plus grosse faute de l'interprétation de Jobin consiste à y voir un tempérament à deux tierces pures, ce qui lui donne un aspect très français, avec plusieurs quintes plus grandes que pures. Il reconnaît d'ailleurs qu'il s'apparente à D'Alembert. Mon tableau des tempéraments (ci-dessus) montre d'ailleurs une similitude frappante de l'interprétation de Jobin avec le tempérament de Rameau (Nouveau système de musique théorique, Paris 1726, pp107). Son texte est un peu obscur. mais Gallimard en 1754 en donne une interprétation quantifiable reproduite ici en chiffres gras (voir D. Devie, le Tempérament Musical p.98, fig.34). Les chiffres en gras de Rameau et de Jobin n'ont rien à voir avec ceux de Bradley Lehmann, qui eux montrent une parenté avec les systèmes Tartini,Valotti ou Young où le comma est réparti sur 6 quintes réduites de 1/6, ce qui ne donne aucune tierce pure.
On sait d'après Marpurg (Versuch
über die Musikalische Temperatur) que Bach demandait à Kirnberger
qu'il rendit larges TOUTES les tierces majeures. Même si cette relation
est en contradiction avec les écrits théoriques de Kirnberger,
qui choisit quand même une tierce pure do-mi pour construire ses tempéraments,
il paraît incohérent de faire dire à la spirale : deux tierces
pures (do-mi puis sol-si) si l'on décide comme Jobin que la double boucle
 correspond à la correction
au 1/4 de comma. Ce choix de deux tierces pures rend inutilisable de nombreuses
tonalités éloignées, ce qui est en contradiction avec l'œuvre
qui parcourt les 24 tonalités. Depuis deux cents ans, de nombreux musicologues
ont prôné l'égalité parfaite pour le clavier bien
tempéré. Le génie de Lehman , c'est d'avoir lu cette spirale
comme un Tartini-Valotti adouci (il n'y a plus que 3 ou 4 quintes pures au lieu
de 6 dans le Tartini Valotti) qui rend toutes les tonalités sympathiques,
mais avec leur propre caractère, à l'inverse du tempérament
égal.
correspond à la correction
au 1/4 de comma. Ce choix de deux tierces pures rend inutilisable de nombreuses
tonalités éloignées, ce qui est en contradiction avec l'œuvre
qui parcourt les 24 tonalités. Depuis deux cents ans, de nombreux musicologues
ont prôné l'égalité parfaite pour le clavier bien
tempéré. Le génie de Lehman , c'est d'avoir lu cette spirale
comme un Tartini-Valotti adouci (il n'y a plus que 3 ou 4 quintes pures au lieu
de 6 dans le Tartini Valotti) qui rend toutes les tonalités sympathiques,
mais avec leur propre caractère, à l'inverse du tempérament
égal.
De plus les tempéraments germaniques présentent la particularité d'être des cycles de quintes pures dans lesquels, pour fermer le cercle, on a inclus des quintes réduites totalisant une altération de 1 comma pythagoricien. D'où le qualificatif d'irrégulier donné à ces tempéraments. Voir les explications détaillées sur le site http://perso.wanadoo.fr/organ-au-logis/Pages/Temperam.htm
C.P.E. Bach nous le rappelle dans le Versuch :
§ 14. Les deux types d’instrument -clavecin et clavicorde- doivent être bien tempérés, étant donné que par l’accord des quintes et octaves et par l’écoute des tierces majeures et mineures et des accords complets, on retranche à la plupart des quintes la quantité qu’il faut de leur pureté extrême pour que l’oreille s’en aperçoive à peine, et que l’on puisse bien se servir des vingt-quatre tonalités. En écoutant les quartes on a l’avantage d’entendre plus clairement le battement nécessaire des quintes, parce que les quartes ont leur fondamentale plus basse que les quintes. Si les instruments à clavier sont accordés ainsi, on peut à juste titre les faire passer pour les instruments les plus purs à cause de la pratique, car peu d’instruments sont accordés sans être joués. Sur ces instruments on joue avec une égale pureté des vingt-quatre tonalités, et ceci de manière notoirement polyphonique, bien que l’harmonie mette immédiatement à jour la moindre fausseté à cause des relations. Par cette nouvelle manière de tempérer nous sommes parvenus plus loin que précédemment, bien que l’ancienne était telle que certaines tonalités étaient plus pures que maintenant quand on joue avec d’autres instruments. Chez plus d’un autre musicien on remarquerait plutôt le manque de pureté, sans avoir besoin d’un appareil qui mesure les accords, s’il fallait entendre de manière harmonique les sons produits de manière mélodique. Cette mélodie nous trompe souvent, et nous empêche plutôt de ressentir ses sons faux, jusqu'à ce que cette fausseté s’accroisse au point de rejoindre presque celle d’un instrument mal accordé. (J.P.Coulon, trad.)
Retour à l' index